立銑刀間隙加工工藝的建模與分析

2020-06-20

摘要

銑刀的間隙對銑削的性能影響很大，因此對其加工理論和工藝提出了很高的要求。在分析實際加工工藝的基礎上，引入包絡理論、空間幾何學原理，建立間隙加工模型，同時考慮用於加工凸形、偏心或橢圓形間隙的砂輪的幾何形狀、方向和位置。相應的，討論了加工所需間隙的砂輪幾何形狀和位置的限制。使用帶有API函數編程的商業計算機輔助設計系統來實現加工過程的可視化。最後得到實體模型。

1. 簡介

間隙角是立銑刀最重要的結構之一。它影響著刀刃的強度和鋒利度、銑刀壽命以及加工表面的質量。但對立銑刀製造工藝的研究主要集中在螺旋槽磨削工藝上。對間隙磨削工藝的分析很少。

在很多情況下，間隙是在溝槽設計過程中設計和計算出來的，其依據是假設在端銑的橫截面上是一條直線。顯然，用這種方法建立的間隙模型不能準確反映實際加工情況。崇以不同的研究思路，描述了立銑刀間隙的重磨工藝。強調了偏心間隙重磨工藝的原理，包括重磨順序、端銑、砂輪、齒託的位置。在五軸數控刀具磨床的基礎上，Chen等人利用刀具磨削CAM系統對間隙的磨削工藝進行了規劃。介紹了磨床各軸在平、凹、偏心加工過程中的平移和旋轉順序。 Uhlmann等人用杯形砂輪加工了多個間隙面，並討論了所用砂輪金剛石晶粒尺寸的影響。此外，其他一些研究者也提到了間隙加工技術。但是，這些研究並沒有詳細介紹如何建立間隙加工工藝的數學模型。

本文根據實際加工工藝、包絡理論和空間幾何建模技術原理，詳細介紹了間隙加工工藝。計算了砂輪幾何形狀、方向和位置的數學模型。強調了偏心間隙加工過程中的原理和問題。據此，利用UG二次開發技術，開發了間隙加工工藝仿真系統。此外，還進行了凸、偏心、橢圓間隙加工工藝的實例。

2. 間隙加工工藝

根據砂輪類型和磨削工藝的不同，立磨的間隙幾何形狀一般分為三種：平型、偏心、凸型（圖1）。平面間隙是最常見的端磨形狀。如圖1a所示，採用杯形或錐形砂輪，與立銑的相對位置如圖所示。開始時，砂輪軸線(n1)與立磨軸線垂直。為了避免因接觸面積過大而造成的燒磨現象，再將砂輪旋轉。因此，平面間隙主要由砂輪圓周研磨。偏心間隙與其他兩種形狀相比，強度更高，端磨壽命更長。一般用圓柱砂輪加工，其軸線(n2)與立銑刀的軸線共面(圖1b)。要磨削間隙角，兩軸之間必須有一定的角度(φ2)。凸形間隙的強度最小。另一方面，它的加工工藝最簡單。圖1c給出了砂輪相對於端銑的位置。砂輪軸(n3)與立銑刀軸平行，其位置可由間隙角α0推算。

在實際工作中，間隙面的磨削過程通常是從刀柄側到端齒的過程。為了計算方便，本文所有工序均從端齒開始，不會影響加工效果。

3. 平面間隙加工工藝

如圖2所示，坐標系XgYgZg代表砂輪架，XYZ代表固定的端銑架。本文只在螺旋槽磨削後加工間隙，刀尖位於坐標(mR，0，0)處，方程以端銑架表示。

圖3為平面間隙加工中砂輪坐標系的變換程序。假設砂輪坐標系在開始時與端銑坐標XYZ重合，坐標系XgY gZ g可由O分別沿X軸和Z軸的兩個平移參數mR和-gR推導出。將砂輪架XgY gZ g繞其Zg軸旋轉一個角度α0（得到坐標系Xg1Y g1Z g1），可以加工出數值為α0的平面間隙角。為了避免因砂輪與間隙接觸面積過大而造成的磨削燒傷現象，再將砂輪以φ1的角度旋轉到坐標系Xg2Y g2Z g2（圖3）。現在，就可以得到砂輪相對於端銑的初始位置。砂輪的方向可以用下面的矢量來表示。.

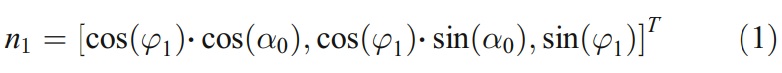
而砂輪的位置可以用以下方式表示

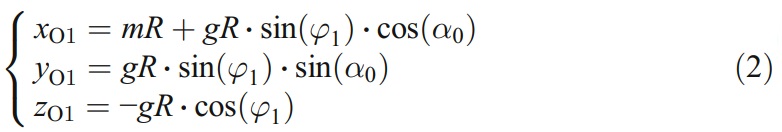
4 偏心間隙加工工藝

4.1 加工原理

根據圖1b提供的砂輪位置，建立坐標來表示砂輪的初始位置，開始加工過程（圖4）。參數φ2為砂輪架關於其Xg軸的旋轉角度。砂輪的方向可以由矢量給出

而砂輪的位置可以表示為

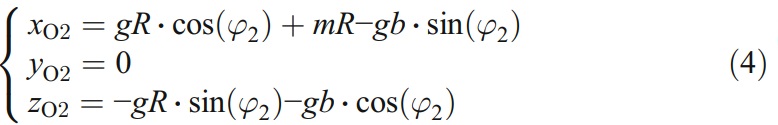
圖5a給出了偏心加工過程中砂輪相對於端銑的位置。從加工結果可以看出，磨削加工後有兩個面：一個是砂輪圓柱面所包圍的間隙面，另一個是砂輪圓周所產生不需要的面。圖5b為基於圖1b的加工結果（即點p4與點Q重合，gb=10mm）。P1為接觸線與端銑輪廓的交點。P2為接觸線與砂輪圓周的交點。 P3為端銑輪廓與砂輪圓周的交點。

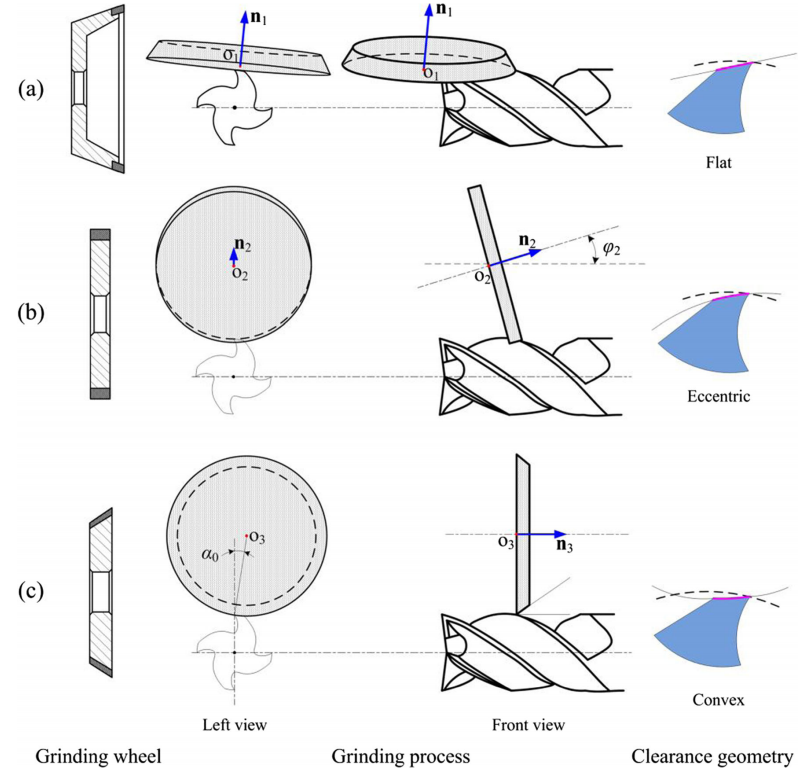
圖1 平形、偏心、凸形間隙的加工過程

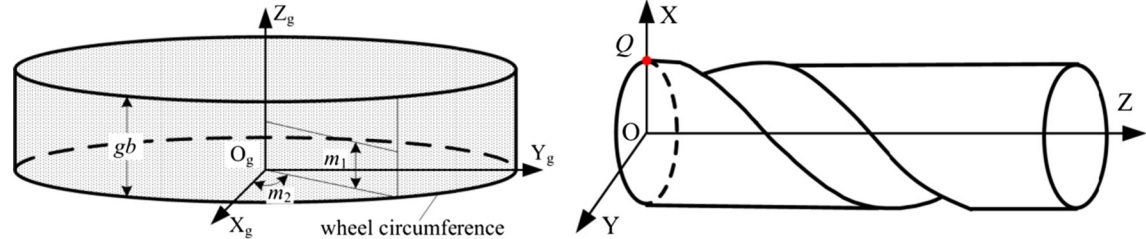
圖2 砂輪和端銑計算的坐標 (a) 砂輪坐標 (b) 端銑坐標

顯然，從圖中可以看出兩個問題：包絡面邊界(即間隙面邊界)與切削刃不重合，當Φ'>Φ時，不需要的加工面會影響其他齒面。另外，傾斜角φ2和間隙角α0至今無法計算。為了解決這三個問題，下面將進一步詳細研究。

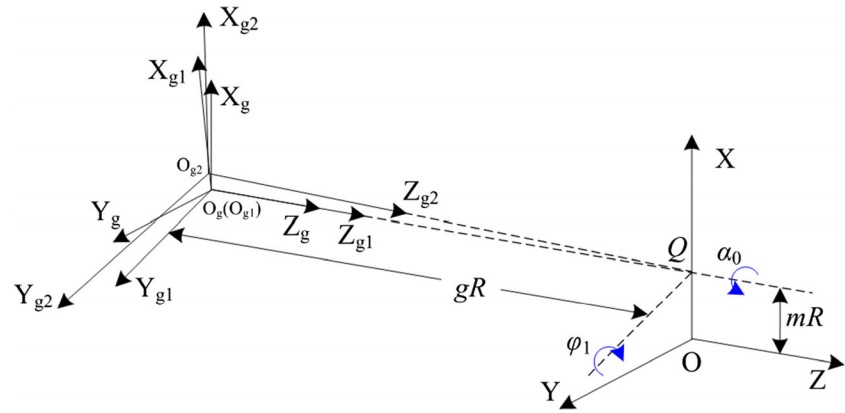
圖3 平面間隙加工中砂輪坐標系的變換程序

4.2 清除面邊界分析

由圖5b可知，只要點p1位於切削刃上，包絡面邊界將與切削刃重合。根據公式(3)和(4)，如圖4所示，砂輪的圓柱面可以用這種形式表示為

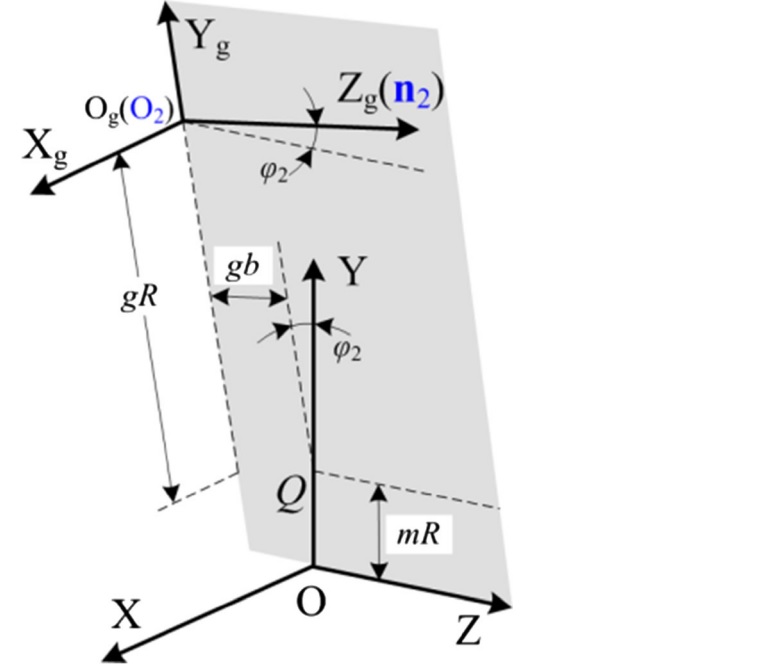
圖4 偏心間隙加工中車輪坐標系的變換程序

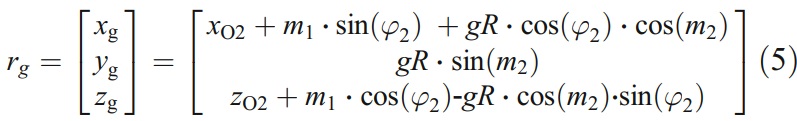
那麼，沿著切削刃移動砂輪，以恆定的導程P，就可以得到一個砂輪面族，並表示成

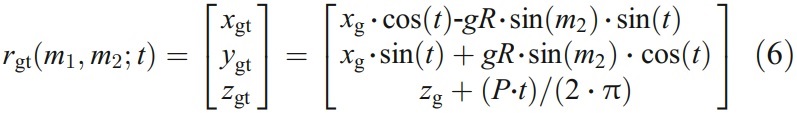
其中t代表砂輪繞端銑軸線移動的旋轉角度。根據包絡原理，形成間隙加工的基本關係為

(∂rgt/∂m1,∂rgt/∂m2,∂rgt/∂t)=0

其中

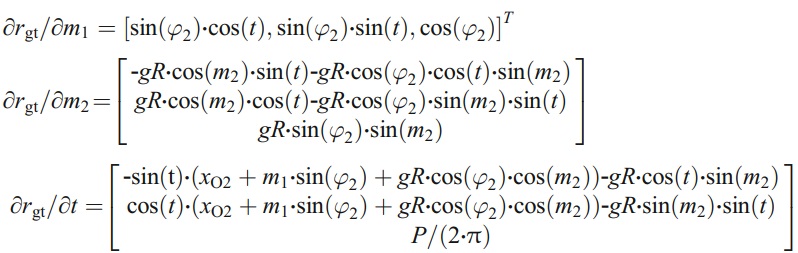
它可以簡單地表示為

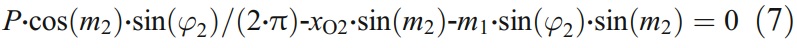
或是

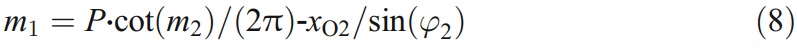
現在，由研磨過程得出的包絡方程表示為式（7），其中m1∈[0，gb]和m2∈[0，2π]。

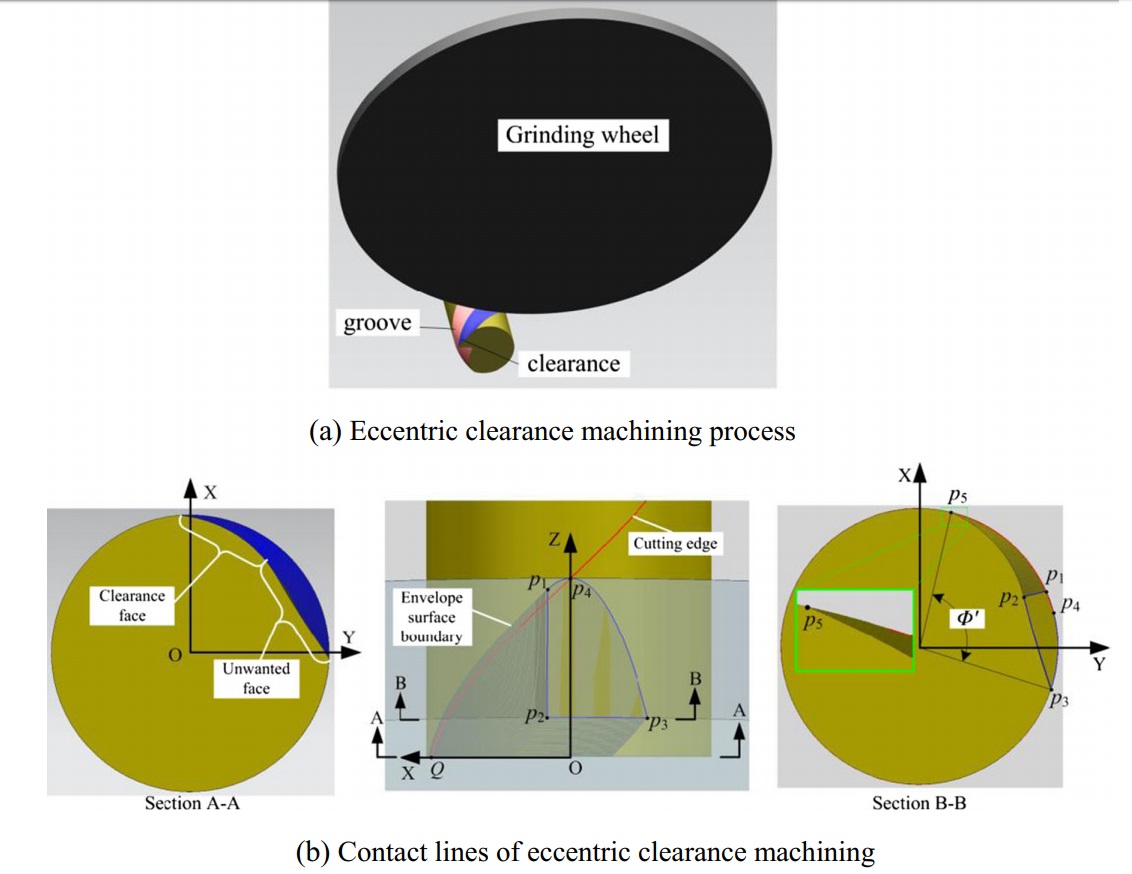
圖5 偏心間隙加工機構。(a)偏心間隙加工過程。(b)偏心間隙加工的接觸線

將式(8)和t=0代入式(6)，得到砂輪的接觸線(即線p1p2)和初始加工位置的間隙，其形式為

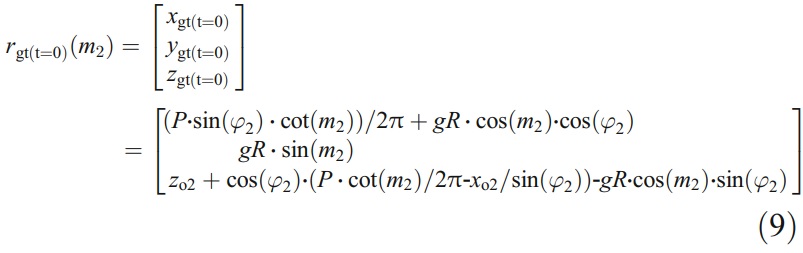
最後，p1的坐標(xp1,yp1,zp1)可以通過解方程x 2 gt(t=0)+y 2 gt(t=0)=mR2來計算。為了使包絡面邊界與切削刃重合，必須在開始時將點p1移至點p4（即t=0，點p4與點Q重合）。因此，在加工過程前，砂輪應

表1 偏心間隙製造的工藝參數

從架構XgYgZg隨Z軸移動旋轉（如圖4所示），角度為λ，位移為|zp1|。其中，λ為X軸與Op1在端銑截面上的投影線的夾角，可表示為

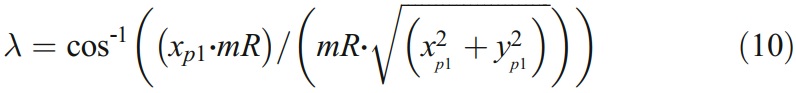
表2 接觸線上的點

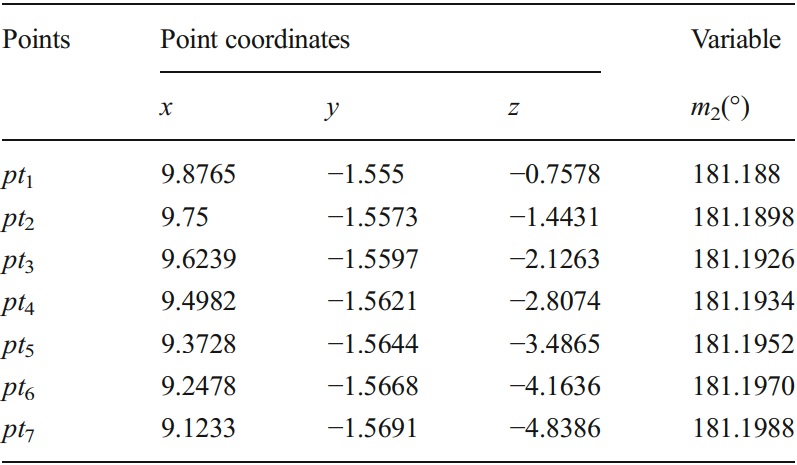
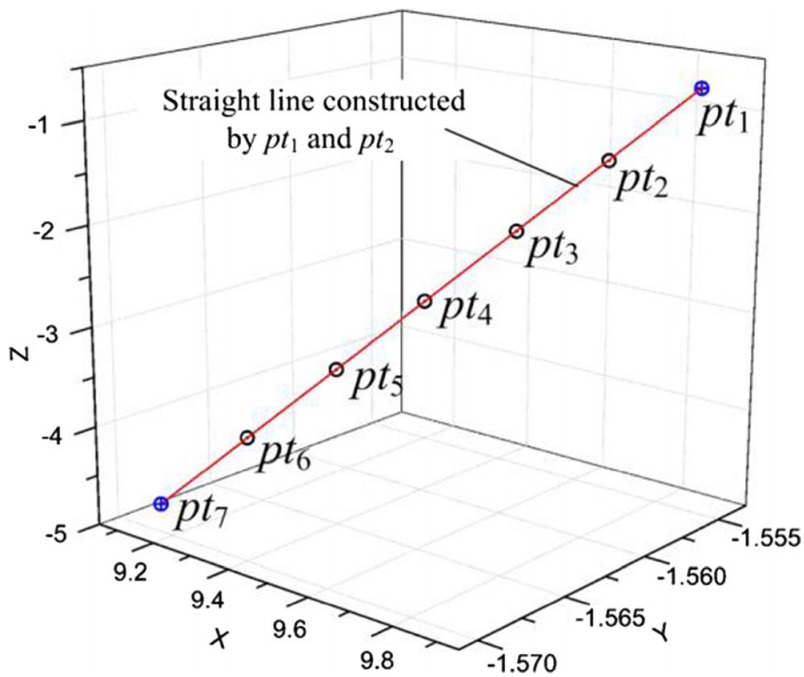
圖6 接觸線上的點 pt1pt2

4.3 傾角的定義

將表1中列出的參數代入式(9)，可以計算出接觸線上的各點。結果如表2所示。圖6顯示了三維坐標中各點的位置。將第一點和最後一點(pt1和pt7)用直線連接起來，發現其他點都在直線上，這說明接觸線也是一條直線。

據圖5b，用圖7表示φ2和α0的關係，得出以下公式:

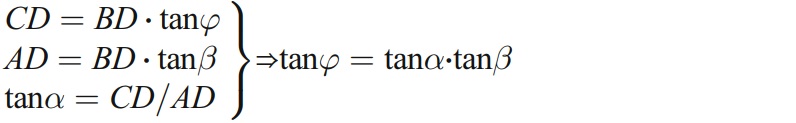
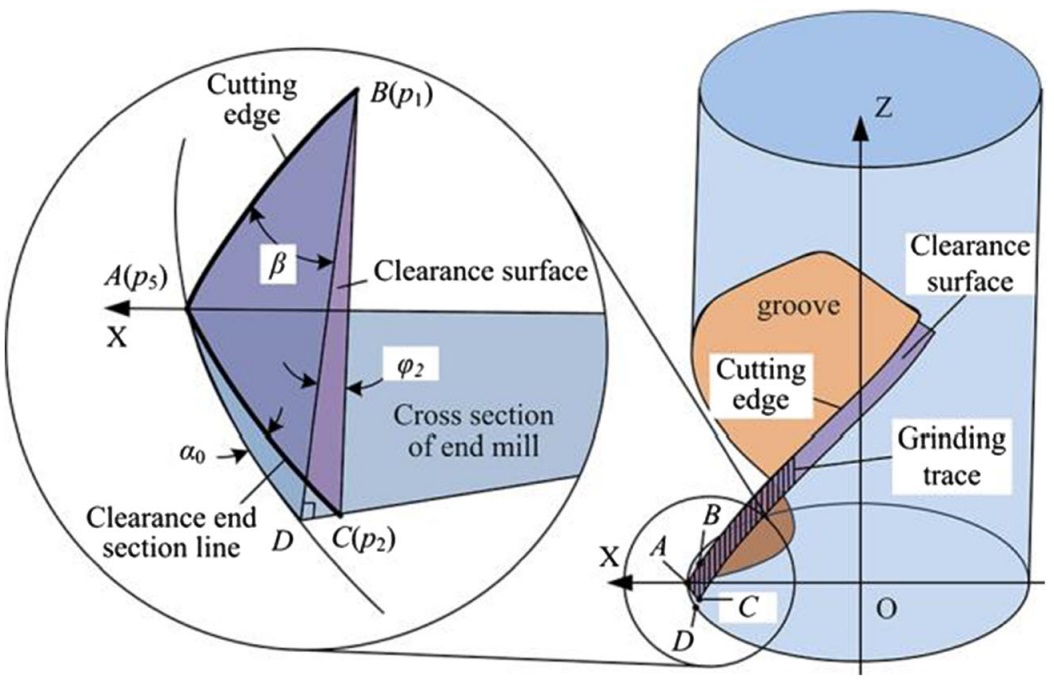
圖7 間隙角(α0)與安裝角(φ2)之間的關係

由此不難看出

這個方程表明，傾角φ2只取決於螺旋角β和間隙角α0。

4.4 不干擾條件

很明顯，只有當角度Φ'小於Φ時，才能加工出無干涉的間隙。從圖5b中得知，角度Φ'是由線p1p2和線p2p3在端面銑的截面上產生的。所以，在接下來的研究中，角度Φ'的計算分為兩部分。

①分析線p1p2所產生的曲面，將zgt=0代入式(6)中，可推導出關係為

現在，將式(8)和式(12)代入式(6)中，可得到由線p1p2在端面銑刀橫截面上產生的加工輪廓(圖5b中的p2p5)的方程，然後通過求解加工輪廓和端面銑刀輪廓的方程，計算出點p5的坐標(xp5,yp5,0)。然後，通過求解加工輪廓和端銑輪廓的方程，可以計算出點p5的坐標(xp5,yp5,0)。

②線p2p3產生的曲面分析將m1=0代入式(6)中，得到輪圓周沿切削刃運動產生的螺旋曲面，其形式為

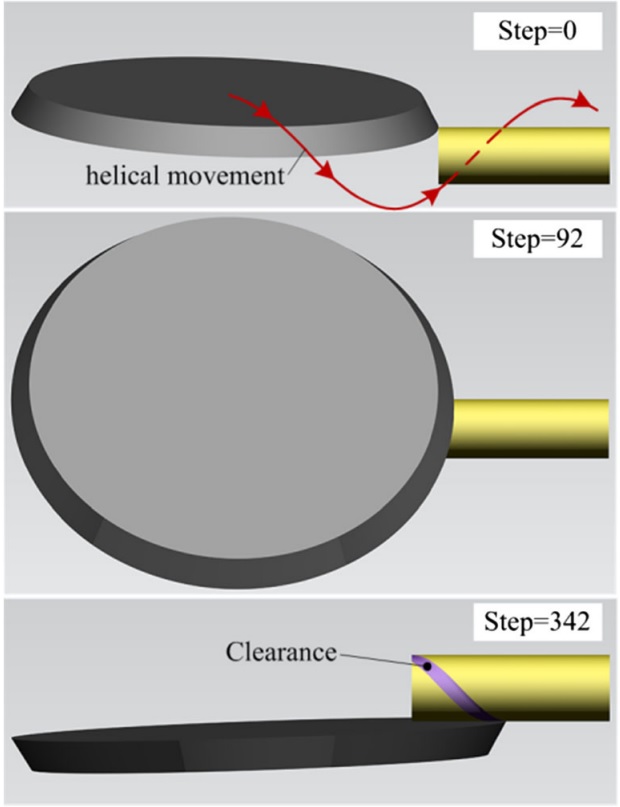
圖8 間隙加工過程模擬

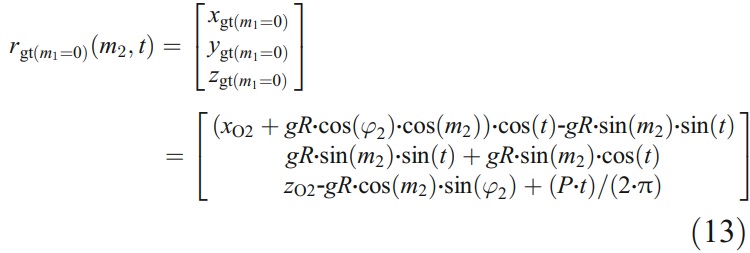
通過解方程zgt(m1=0)=0，可以得出函數t= f2(m2)。將其代入式(13)，可得到端銑截面上的線p2p3所產生的加工輪廓方程。現在，推導出點p3的坐標（xp3,yp3,0）。根據點p5和p3的坐標，角Φ'可以表示為

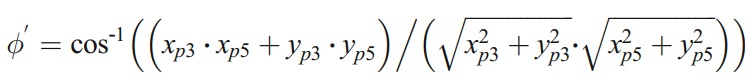
③簡化算法

上述方法可以得到Φ'的精確值，但計算過程非常複雜。由於Φ'的角度並不影響間隙的幾何形狀，因此，一種快速評估的方法，其解決方法可能有一個允許的誤差，在實踐中會更有用。

圖9 平面間隙加工時砂輪的初始位置

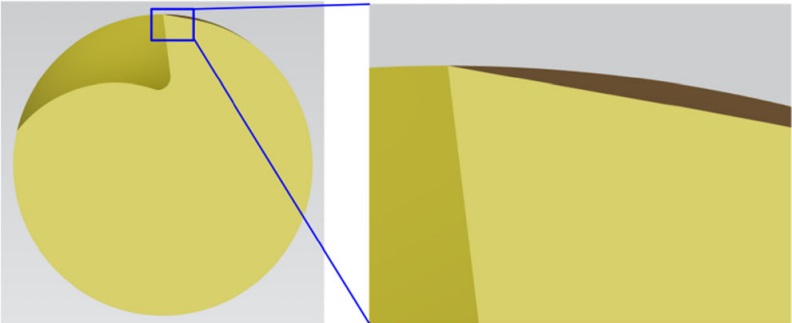
圖10 平面間隙加工的仿真結果

根據圖7，線p1p2在立銑刀截面上產生的加工輪廓可以表示為一段圓弧SAD，其定義為

sAD = BD⋅tanβ = gb⋅cos (φ2) ⋅tanβ

根據圖5b，由線p2p3產生的加工輪廓可以近似地用以下形式表示

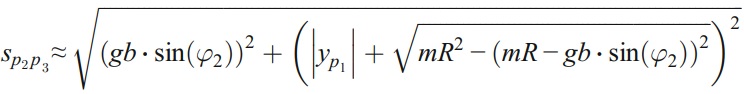
現在，角Φ'可以用以下公式表示

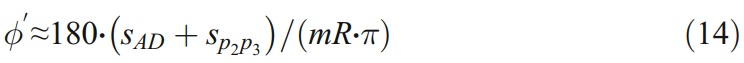
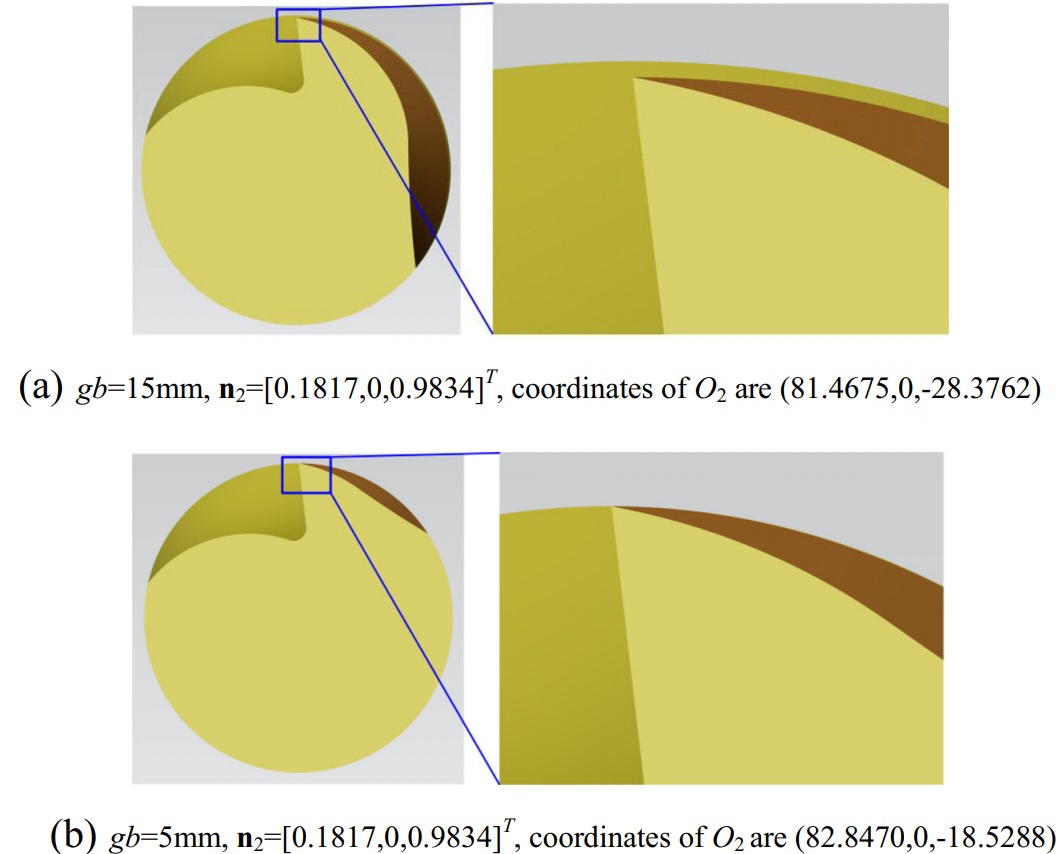
圖12 偏心間隙加工仿真結果。(a) gb=15 mm，n2=[0.1817,0,0.9834]T，O2的坐標為(81.4675,0,-28.3762)。(b) gb=5 mm，n2=[0.1817,0,0.9834]T，O2的坐標為(82.8470,0,-18.5288)

5. 凸面間隙加工工藝

如圖1c所示，用於加工凸面間隙的砂輪方向很容易得到，其形式為

n3 = [0, 0, 1] T

而砂輪架的原點位於坐標(xo3,yo3,zo3)

圖13 凸面間隙加工時砂輪的初始位置

6. 範例

為了驗證上述建立的數學模型，UG二次開發技術建立了間隙磨削仿真係統。在仿真過程中，就像實際磨削過程一樣，砂輪沿著螺旋線（即螺旋切削刃）一步一步地移動。每一步都採取布爾減法運算：砂輪為 "刀具"，毛坯為 "目標"。那麼，通過這些布爾運算就可以建立間隙模型（圖8）。

以參數為mR=10 m、p=60 mm、α0=10°的立銑刀為例，驗證數學模型。例子中使用的砂輪半徑為75mm

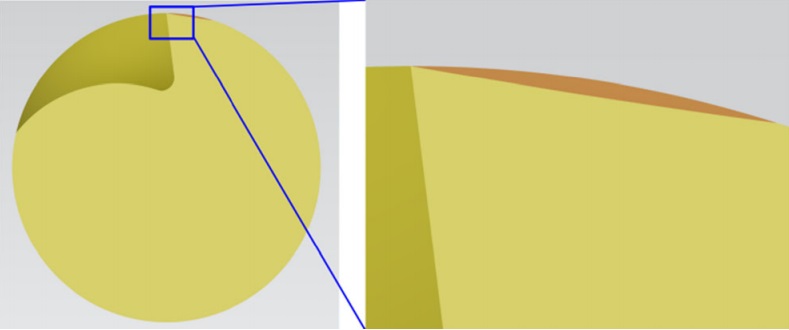
圖14 凸面間隙加工的仿真結果

6.1平面間隙加工實例

將φ1=2°代入式(1)和式(2)，可計算出砂輪的方向為n1=[0.98,0.17,0.03]T，O1的坐標為(12.58,0.45,-74.95)。仿真過程如圖9所示，結果如圖10所示。

6.2 偏心間隙加工實例

根據公式(11)，可推算出加工偏心間隙的砂輪傾角(φ2)為10.4675°。圖11為仿真過程。

將gb=15mm代入式(3)和式(4)，可計算出砂輪位置參數為n2=[0.1817,0,0.9834]T，O2的坐標為(81.4675,0,-28.3762)。根據公式(14)，可計算出角Φ'(圖5b)為142.53°。仿真結果如圖12a所示。顯然，當Φ<Φ'時，會出現干涉現象(即四齒以上的立銑刀無法正常加工)。此外，切削刃與包絡面邊界不一致，會出現過切現象。

根據式(9)和式(10)，推算出p1的坐標為(9.8784,-1.5550,-0.7476)，λ等於8.9458°。從框架XgYgZg(如圖4所示)沿Z軸旋轉和移動砂輪(如圖4所示)，8.9458°和0.7476毫米，並將gb從15毫米減少到5毫米，可以得到新的模擬結果(圖12b)。現在，只要相鄰刀角Φ大於62.39°(因為Φ'=62.39°)，就可以正常磨削間隙。

6.3 凸形間隙加工實例

根據式(15)可計算出O3的坐標為(81.4675,0,-28.3762)。仿真過程和結果如圖13和圖14所示。

7. 結論

在實際工藝分析的基礎上，建立了加工平面、偏心、凸形間隙的數學模型。計算了砂輪的方向和位置，討論了加工所需間隙的條件。此外，還開發了一個仿真系統來驗證數學模型，並將加工過程可視化。主要結論總結如下。

1. 舉例說明，正確推導出間隙加工的數學模型。
2. 對於偏心間隙加工，可以通過減小砂輪厚度來解決相鄰切削刃的欠切問題。另外，為了加工出理想的偏心間隙，包絡面邊界應與切削刃重合，這就導致在開始加工前，需要對砂輪進行額外的變換。
3. 仿真程序得到的間隙是實體模型，可以作為有限元分析的輸入模型。

致謝

該項目是國家科技重大專項項目（編號：2012ZX04003-021）和 "山東省泰山學者計劃基金 "支持項目。